Functors Between Real and Complex Vector Spaces
(Unfinished)
In Chapter 12, R.G. describes three possible transformations “from real to complex vector spaces and back”. Inspired by Chapter 17 (Functors), I have examined these transformations from the functor point of view.
We can distinguish not two, but three categories here, the first and third of which are equivalent:
 : Complex vector spaces with their usual morphisms and composition law.
: Complex vector spaces with their usual morphisms and composition law.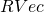 : Real vector spaces with their usual morphisms and composition law.
: Real vector spaces with their usual morphisms and composition law.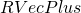 : The category of pairs
: The category of pairs 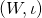 , where
, where  is a real vector space and
is a real vector space and  a vector space morphism
a vector space morphism 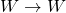 such that
such that  (with
(with  the identity morphism on
the identity morphism on  ). A morphism
). A morphism 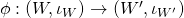 in this category is any linear mapping from
in this category is any linear mapping from  to
to  subject to the condition:
subject to the condition: 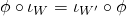 . These morphisms are composed as mappings. It is simple to check that this does make up a category.
. These morphisms are composed as mappings. It is simple to check that this does make up a category.
Equivalence of  and
and 
The equivalence of these two categories stems from the procedures described in Chapter 12, procedures that we will describe as isofunctors.
Functor  from
from  to
to 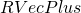
Action on objects:
If ![]() is a complex vector space,
is a complex vector space, ![]() is such that:
is such that:
 is the real vector space obtained from
is the real vector space obtained from 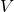 by “forgetting” multiplication by imaginaries, that is the one based on the same set as
by “forgetting” multiplication by imaginaries, that is the one based on the same set as 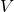 with the same addition, the multiplication by a scalar being simply restricted to real scalars.
with the same addition, the multiplication by a scalar being simply restricted to real scalars. is the linear mapping
is the linear mapping 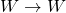 that sends a vector
that sends a vector 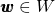 to
to  , the scalar multiplication here being that in the complex vector space
, the scalar multiplication here being that in the complex vector space 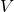 . One immediately checks that we do have
. One immediately checks that we do have  .
.
Action on morphisms:
A morphism between complex vector spaces is also, as a mapping, a morphism between the corresponding real vector space obtained by “forgetting” multiplication by imaginaries; thus, for a ![]() -morphism
-morphism ![]() , we can define
, we can define ![]() as the same mapping. It is simple to check that the condition on
as the same mapping. It is simple to check that the condition on ![]() -morphisms
-morphisms ![]() is satisfied.
is satisfied.
Functor  from
from 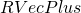 to
to 
The second construction described by R.G. takes a pair ![]() with
with ![]() real vector space and
real vector space and ![]() morphism
morphism ![]() such that
such that ![]() to a complex vector space. We can make this into a functor
to a complex vector space. We can make this into a functor![]() from
from ![]() to
to ![]() by defining what happens to morphisms: they are left as they are, as mappings; the above condition on morphisms in
by defining what happens to morphisms: they are left as they are, as mappings; the above condition on morphisms in ![]() ensures that the resulting mapping is a
ensures that the resulting mapping is a ![]() -morphism.
-morphism.
These two functors are isofunctors
It is easy to check (R.G. should at least mention it – criticism) that these two operations are the inverse one of the other, which makes ![]() an isofunctor with
an isofunctor with ![]() its inverse, and
its inverse, and ![]() and
and ![]() equivalent categories.
equivalent categories.
Taking free objects between these categories yields nothing new, as we saw in the post on isofunctors.
The main interest in this category ![]() is that it allows us to work with real vector spaces only, avoiding in particular the need to consider complex and real versions of a given vector space, with the scalar multiplication in the former that «knows how» to multiply by complex numbers, while it does not in the latter. In the rest of this post I will talk of complex vector spaces and these «real plus» vector spaces as if they were the same thing.
is that it allows us to work with real vector spaces only, avoiding in particular the need to consider complex and real versions of a given vector space, with the scalar multiplication in the former that «knows how» to multiply by complex numbers, while it does not in the latter. In the rest of this post I will talk of complex vector spaces and these «real plus» vector spaces as if they were the same thing.
Forgetful functor 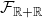 from complex to real vector spaces
from complex to real vector spaces
One can make a forgetful functor ![]() from
from ![]() to
to ![]() simply by forgetting the
simply by forgetting the ![]() part. The functor leaves morphisms unchanged. This is the first construction described by R.G. in Chapter 12, from
part. The functor leaves morphisms unchanged. This is the first construction described by R.G. in Chapter 12, from ![]() to
to ![]() .
.
A sort of inverse construction of 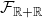
The functor ![]() forgets the
forgets the ![]() , which cannot be retrieved. It can, however, be reinvented, though in general there is a necessary arbitrariness in the process.
, which cannot be retrieved. It can, however, be reinvented, though in general there is a necessary arbitrariness in the process.
Let ![]() be a real vector space. Suppose that it is possible to find in
be a real vector space. Suppose that it is possible to find in ![]() two subspaces,
two subspaces, ![]() and
and ![]() , that are complementary and isomorphic. There will in general be an infinite number of ways of choosing the pair
, that are complementary and isomorphic. There will in general be an infinite number of ways of choosing the pair ![]() , and, this pair being chosen, an infinite number of ways of choosing and isomorphism
, and, this pair being chosen, an infinite number of ways of choosing and isomorphism ![]() . (One can, for instance, arbitrarily choose bases on
. (One can, for instance, arbitrarily choose bases on ![]() and
and ![]() , and create
, and create ![]() from an arbitrary bijection between these bases.)
from an arbitrary bijection between these bases.)
![]() is a mapping between two specific subspaces of
is a mapping between two specific subspaces of ![]() . We can, however, create a full mapping
. We can, however, create a full mapping ![]() by posing:
by posing:
![]()
It is easy to check that this ![]() is linear, and that
is linear, and that ![]() . Hence
. Hence ![]() is an object of
is an object of ![]() . Applying the
. Applying the ![]() functor defined above, we obtain a complex vector space.
functor defined above, we obtain a complex vector space.
The necessary and sufficient condition for it to be possible to find in ![]() two complementary and isomorphic subspaces is that
two complementary and isomorphic subspaces is that ![]() be either finite and even-dimensional, or infinite-dimensional (exercise 84).
be either finite and even-dimensional, or infinite-dimensional (exercise 84).
Providing this condition is satisfied, this procedure involves the arbitrary step of choosing the subspaces, and the second arbitrary step of choosing the isomophism between them. For this reason, one cannot make it into a functor; for a functor must consist of a rule for mapping objects and morphisms. We don’t have an inverse functor for ![]() .
.
This arbitrariness is present even in the simplest non-trivial case, that of a two-dimensional real vector space. This is another formulation of the fact that in a complex vector space there is no non-arbitrary notion of “real” and “imaginary” vectors (as noted in Chapter 12).
Free objects following the forgetful functor from complex to real vector spaces
We do, however, have a functor from ![]() to
to ![]() , but one that implies doubling the initial vector space. It uses the third construction described in Chapter 12.
, but one that implies doubling the initial vector space. It uses the third construction described in Chapter 12.
It is simpler to talk of this construction with ![]() rather than
rather than ![]() ; we have seen that these categories are equivalent. Given an object
; we have seen that these categories are equivalent. Given an object ![]() in
in ![]() , that is, a real vector space, we take
, that is, a real vector space, we take ![]() as the real vector space direct sum
as the real vector space direct sum ![]() . We define the mapping
. We define the mapping ![]() by
by ![]() . It is easy to check that
. It is easy to check that ![]() is linear, and that
is linear, and that ![]() . Hence
. Hence ![]() is an object in
is an object in ![]() . We thus have a rule
. We thus have a rule ![]() that maps objects of
that maps objects of ![]() to objects of
to objects of ![]() . Now let us consider a morphism
. Now let us consider a morphism ![]() in
in ![]() , between real vector spaces
, between real vector spaces ![]() and
and ![]() . Let
. Let ![]() and
and ![]() . We can form the mapping
. We can form the mapping ![]() . It is linear, and furthermore
. It is linear, and furthermore ![]() ; hence
; hence ![]() is a morphism in category
is a morphism in category ![]() , between
, between ![]() and
and ![]() . We write
. We write ![]() . We can check that this rule
. We can check that this rule ![]() preserves composition and identities. It is thus a functor from
preserves composition and identities. It is thus a functor from ![]() to
to ![]() .
.
Now let us examine if this ![]() cannot be viewed as the — or better, a — free object functor following functor
cannot be viewed as the — or better, a — free object functor following functor ![]() .
.
Let ![]() be a real vector space, and
be a real vector space, and ![]() , that is
, that is ![]() and
and ![]() .
. ![]() and
and ![]() are objects in
are objects in ![]() . Let
. Let ![]() be the
be the ![]() -morphism
-morphism ![]() defined by
defined by ![]() . We wish to check that
. We wish to check that ![]() is a free object on
is a free object on ![]() following
following ![]() and that the transformation of morphisms follows suit.
and that the transformation of morphisms follows suit.
Let ![]() be another object of
be another object of ![]() and
and ![]() a
a ![]() -morphism from
-morphism from ![]() to
to ![]() , that is a linear mapping
, that is a linear mapping ![]() .
.
We wish to find a ![]() -morphism
-morphism ![]() such that
such that ![]() . But
. But ![]() is just the mapping
is just the mapping ![]() itself. For
itself. For ![]() ,
, ![]() . So
. So ![]() must map any
must map any ![]() to
to ![]() . Since
. Since ![]() must also be a
must also be a ![]() -morphism, we must have
-morphism, we must have ![]() .
.
In other words, necessarily, our ![]() must be such that
must be such that ![]() .
.
Now we must check that ![]() thus defined is indeed a
thus defined is indeed a ![]() -morphism
-morphism ![]() and that
and that ![]() (for up to now we have shown what
(for up to now we have shown what ![]() must be; we must check that the result is indeed adequate). This checking is unproblematic.
must be; we must check that the result is indeed adequate). This checking is unproblematic.
Thus our ![]() is a free object on the real vector space
is a free object on the real vector space ![]() following the functor
following the functor ![]() .
.
But it’s not quite over! We must also check that, taking