“Free Object Functors”

olivierd

Jun 26, 2017 4 min read

“Free Object Functors”

Chapter 12 (Functors) gives as an example of a functor the “free group functor” from the category of sets ( $Set$ ) to the category of groups ( $Grp$ ). We will call this functor $\mathcal G$ , and its construction, as described, is the following:

For any set $S$ , the object $\mathcal G(S)$ is the free group on $S$ .

Let $\phi$ be a $Set$ -morphism, that is, any mapping, between sets $S_1$ and $S_2$ . Let $G_1$ and $G_2$ be the respective free groups, with $\alpha_1: S_1 \to G_1$ and $\alpha_2: S_2 \to G_2$ the associated mappings.

Then, by virtue of the universal property of free groups, there exists a unique $Grp$ -morphism $\psi: G_1 \to G_2$ such that, as mappings, $\psi \circ \alpha_1 = \alpha_2 \circ \phi$ .

So we decide that $\mathcal G(\phi)$ will be this $\psi$ . Of course, for this to be a functor, we must check that the composition of morphisms are preserved, as are identities.

Later in the chapter, the general concept of a free object in category $\mathcal C'$ on an object in $\mathcal C$ via a functor $\mathcal F$ from $\mathcal C'$ to $\mathcal C$ is defined, as an extension of the notion of a free group; a free group thus becomes the free object in category $Grp$ on an object in category $Set$ following the forgetful functor $\mathcal F$ from $Grp$ to $Set$ . We are called to consider the “free object functor” from $\mathcal C$ to $\mathcal C'$ (hence in the reverse direction respective to $\mathcal F$ ), based as above on the mapping of objects in $\mathcal C$ to their respective free objects in $\mathcal C'$ and of $\mathcal C$ -morphisms to the corresponding $\mathcal C'$ -morphisms following the above construction.

This set-up at first appears clear, but left me feeling uneasy. After some thought I managed to pinpoint two issues:

Free objects, when they exist, are unique up to an isomorphism, which means that they aren’t «unique, period». For a functor to map a set to its free group, one must have a rule that says what exactly that group is; you can’t just say what it is up to an isomorphism.
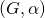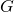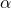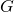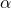«Free objects» are not actually objects in the target category; they are ordered pairs $(G, \alpha)$ , where $G$ is an object of the target category, that is, in our example, groups, and $\alpha$ is a morphism between objects of the source category. If I build a free group functor retaining only the target object, in our case $G$ , the $\alpha$ part is lost.

The first issue can be solved easily for groups, and, I suspect, in most or all other cases. The existence of a free object is usually (always?) demonstrated by building some particular instance; one can decide that the functor will map the source object to that specific free object, that we will call the canonical free object.

For the second issue, one must note that the associated morphisms $\alpha$ is not complete. We need these $\alpha$ to build $\mathcal G(\phi)$ from $\phi$ . Thus the $\alpha$ ‘s remain at least partly included in the definition of the free group functor.

I don’t have the impression that if we are given the functor $\mathcal G$ , without the knowledge of the canonical free groups that it is built upon, we can reconstruct the $\alpha$ morphisms that are part of the definition of thise canonical free objects. The picture is rather this:

We define a particular rule for building a free group 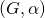$(G, \alpha)$ on any set $S$ .
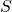Based on this rule, we define the mappings from objects in $Set$ to objects in $Grp$ , and from morphisms in $Set$ to morphisms in $Grp$ .
The entire above procedure (including the rule for building a specific free group) constitutes our free group functor, that is our rule for mapping $Set$ to $Grp$ and morphisms in $Set$ to morphisms in $Grp$ .

In practice, it doesn’t matter much what particular rule we take for building our free objects. It does matter, however, that it be conceived of as well specified, and that we understand that not only the $G$ part but also the $\alpha$ in the free object serve to define the free object functor.

criticism