The composition of polynomials
Definition
Let ![]() be a commutative field. The polynomials
be a commutative field. The polynomials ![]() form a commutative unital algebra over
form a commutative unital algebra over ![]() containing an element
containing an element ![]() such that the following universal property holds:
such that the following universal property holds:
For any unital algebra ![]() (commutative or otherwise) and any element
(commutative or otherwise) and any element ![]() , there exists exactly one unital algebra morphism
, there exists exactly one unital algebra morphism ![]() such that
such that ![]() .
.
If ![]() and
and ![]() are elements of
are elements of ![]() , let
, let ![]() be the unique morphism such that
be the unique morphism such that ![]() . Then the composition
. Then the composition ![]() of
of ![]() and
and ![]() is defined by
is defined by ![]() .
.
Effect of composition of polynomials on the corresponding functions
In terms of polynomial functions, the composition of polynomials is the equivalent to the composition (via “![]() ”) of the associated functions.
”) of the associated functions.
Let us first define the function that is associated with a polynomial.
The set ![]() of functions
of functions ![]() is made into a commutative and unital associative algebra by the usual operations of summing (
is made into a commutative and unital associative algebra by the usual operations of summing (![]() , multiplication by a scalar (
, multiplication by a scalar (![]() and internal multiplication (
and internal multiplication (![]() ).
).
Hence, following the universal property of the algebra of polynomials, there exists a unique morphism ![]() such that
such that ![]() .
.
By definition, the function ![]() associated with a polynomial
associated with a polynomial ![]() is simply
is simply ![]() .
.
We wish to show that if ![]() and
and ![]() are polynomials and
are polynomials and ![]() and
and ![]() the respective associated functions, the function associated with
the respective associated functions, the function associated with ![]() is
is ![]() .
.
Let ![]() be a polynomial and
be a polynomial and ![]() . Let us consider the mapping
. Let us consider the mapping ![]() .
.
It is easy to check that ![]() is a morphism.
is a morphism.
Furthermore, ![]() .
.
On the other hand, ![]() is also a morphism from
is also a morphism from ![]() to
to ![]() , and
, and ![]() .
.
Thus both ![]() and
and ![]() are morphisms
are morphisms ![]() and they agree on the value
and they agree on the value ![]() . The universal property of polynomials entails that they are equal.
. The universal property of polynomials entails that they are equal.
Hence for any ![]() ,
, ![]() .
.
That is, ![]() .
.
Effect on the evaluation of a polynomial
If ![]() and
and ![]() , the evaluation of
, the evaluation of ![]() at
at ![]() is, by definition, the value at
is, by definition, the value at ![]() of the unique morphism
of the unique morphism ![]() such that
such that ![]() .
.
Given polynomials ![]() and
and ![]() and
and ![]() , we wish to evaluate
, we wish to evaluate ![]() at
at ![]() , and, specifically, show that
, and, specifically, show that ![]() .
.
Since ![]() , we have
, we have ![]() .
.
Both ![]() and
and ![]() are morphisms
are morphisms ![]() . Both evaluate at
. Both evaluate at ![]() to
to ![]() . Hence they are equal:
. Hence they are equal:
![]()
which entails ![]()
hence: ![]() , as announced.
, as announced.
In particular: if ![]() and
and ![]() , then
, then ![]() .
.
Associativity
If ![]() ,
, ![]() and
and ![]() are polynomials in
are polynomials in ![]() , we wish to show that:
, we wish to show that:
![]()
Using the definition of composition, this translates into:
![]()
That is:
![]()
We need to show that for any ![]() and
and ![]() in
in ![]() , the two
, the two ![]() mappings
mappings ![]() and
and ![]() are identical.
are identical.
Both are endomorphisms of ![]() .
.
We have:
 by definition of
by definition of 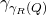 .
. by definition of
by definition of  .
.
Hence both morphisms agree on the image of ![]() . By virtue of the universal property of polynomials, they are equal.
. By virtue of the universal property of polynomials, they are equal.
Hence for any ![]() , we indeed have
, we indeed have ![]() , that is,
, that is, ![]() .
.
Effect of composition on the evaluation of polynomials
todo
Derivation of the composition of polynomials
todo