Representation frameworks and representations
Chapter 22 on representations is, I feel, the worst written I have come upon up to now. I haven’t yet come to wrap my head around it.
I certainly appreciate the desire to give a general definition of representations in category theory terms. This is how the author puts it:
Let
and
be two categories. We suppose that we are given the following two things: i) a forgetful functor
from the category
to the category of sets, and ii) a rule which assigns, to each object
in category
, an object
in category
and an isomorphism (in the category of sets) from set
to the set
.
I see two issues about this setting. I will “correct” these issues in this post, giving what I hope is a better definition, and come to the issue of direct products and sums of representations and of subrepresentations in another post.
About the functor to the category of sets
About the above complex statement, the author reassures us:
There is an obvious forgetful functor from every category we shall consider to the category of sets, and we shall always use this one for item i). The purpose of i) is to allow us to speak of “elements” of objects in category
.
The existence of this “obvious functor” in the categories we consider is very familiar; indeed, groups, vector spaces and so on are built upon sets. We are clearly used to speaking of an element of a group, though in fact we should speak of an element of the underlying set.
Postulating the existence of this forgetful functor ![]() from
from ![]() to
to ![]() is, however, not enough to ensure that we are in the “familiar situation”. There is another element of this familiar situation that is not captured by the mere existence of this functor. Namely: in the familiar situation, the morphisms between objects of
is, however, not enough to ensure that we are in the “familiar situation”. There is another element of this familiar situation that is not captured by the mere existence of this functor. Namely: in the familiar situation, the morphisms between objects of ![]() are no more and no less than morphisms – i.e., mappings – between the corresponding sets. If
are no more and no less than morphisms – i.e., mappings – between the corresponding sets. If ![]() and
and ![]() are objects of
are objects of ![]() , then
, then ![]() is literally a subset of
is literally a subset of ![]() . This implies in particular that
. This implies in particular that ![]() is “one to one” in its action on morphisms; there cannot be two different morphisms
is “one to one” in its action on morphisms; there cannot be two different morphisms ![]() such that
such that ![]() .
.
That this is not necessarily implied by the mere existence of a functor ![]() from
from ![]() to
to ![]() can be made clear by considering this trivial fact: for any category
can be made clear by considering this trivial fact: for any category ![]() , there is a functor
, there is a functor ![]() from
from ![]() to
to ![]() that takes any object
that takes any object ![]() of
of ![]() to the set
to the set ![]() and any morphism in
and any morphism in ![]() between objects
between objects ![]() and
and ![]() to the one and only mapping that exists from set
to the one and only mapping that exists from set ![]() to set
to set ![]() . One can check that this is indeed a functor; but clearly, in general it will take many different morphisms in
. One can check that this is indeed a functor; but clearly, in general it will take many different morphisms in ![]() to just one morphism in
to just one morphism in ![]() .
.
To be closer to the familiar situation, we thus need (at least) the following additional condition: that the functor ![]() from
from ![]() to
to ![]() be “morphism-injective”, that is, such that, for any given objects
be “morphism-injective”, that is, such that, for any given objects ![]() and
and ![]() of
of ![]() and any
and any ![]() , we have
, we have ![]() .
.
We will see why this condition is necessary particularly in the case of the direct products and sums of representations. In the book, it is hidden behind the notations of the author, that tend to muddle the distinction between morphisms in ![]() and the corresponding morphisms in
and the corresponding morphisms in ![]() .
.
Must it really be an isomorphism?
The author postulates that there must be “ii) a rule which assigns, to each object ![]() in category
in category ![]() , an object
, an object ![]() in category
in category ![]() and an isomorphism (in the category of sets) from set
and an isomorphism (in the category of sets) from set ![]() to the set
to the set ![]() “.
“.
It makes for a simpler formulation if instead of speaking of an isomorphism, we say that this rule ![]() must assign to the object
must assign to the object ![]() of
of ![]() an object
an object ![]() of
of ![]() such that
such that ![]() .
.
For instance: if ![]() is the category of real vector spaces, and
is the category of real vector spaces, and ![]() that of real associative algebras, we want our rule
that of real associative algebras, we want our rule ![]() to “make the set of endomorphisms of a given real vector space
to “make the set of endomorphisms of a given real vector space ![]() into an associative algebra”, that is,
into an associative algebra”, that is, ![]() is an associative algebra the underlying set of which is
is an associative algebra the underlying set of which is ![]() .
.
But this doesn’t work well if, instead, we want ![]() to be the category of groups. The author calls this a “special case of the definition of a representaton”, but doesn’t clearly note that in this case, we much change his definition, replacing “isomorphism” by “monomorphism”. In the case of groups, it is not the whole of
to be the category of groups. The author calls this a “special case of the definition of a representaton”, but doesn’t clearly note that in this case, we much change his definition, replacing “isomorphism” by “monomorphism”. In the case of groups, it is not the whole of ![]() that is “made into a group”, but only the set of bijective linear mappings from
that is “made into a group”, but only the set of bijective linear mappings from ![]() to itself.
to itself.
So we will adopt the modified specification of ii): We need a rule ![]() which assigns, to each object
which assigns, to each object ![]() in category
in category ![]() , an object
, an object ![]() such that
such that ![]() .
.
My definition of a representation framework
A representation framework is made of:
- Two categories
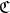 and
and  .
. - A morphism-injective functor from
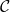 to
to 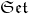 .
. - A rule
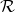 that assigns to each object
that assigns to each object  in category
in category  , an object
, an object  such that
such that  .
.
A representation is…
Given such a representation framework, a representation of an object ![]() of
of ![]() is an ordered pair
is an ordered pair ![]() where
where ![]() is an object of
is an object of ![]() and
and ![]() a
a ![]() -morphism
-morphism ![]() .
.
This is very close to the definition given by the author. He then goes on to state:
(…) for each element ![]() of object
of object ![]() , we must have a certain morphism, which we write
, we must have a certain morphism, which we write ![]() , from object
, from object ![]() to itself.
to itself.
This “
![]() ” is misleading, in that it gives the impression that
” is misleading, in that it gives the impression that ![]() is the image of
is the image of ![]() by
by ![]() . But
. But ![]() is a morphism between
is a morphism between ![]() and
and ![]() . It is not (in general) a mapping at all. It is not
. It is not (in general) a mapping at all. It is not ![]() , but
, but ![]() that is a mapping and can map
that is a mapping and can map ![]() to this
to this ![]() , element of
, element of ![]() .
.
Despite the awkwardness, I will often prefer the notation “![]() ” to the shorter “
” to the shorter “![]() “, because the latter can give rise to the notion that if we happen to have, for each
“, because the latter can give rise to the notion that if we happen to have, for each ![]() , a certain
, a certain ![]() -morphism
-morphism ![]() that we call
that we call ![]() , for instance, then necessarily this mapping forms a
, for instance, then necessarily this mapping forms a ![]() -morphism
-morphism ![]() ; while it only means that we have a mapping of sets
; while it only means that we have a mapping of sets ![]() ‑ if indeed the
‑ if indeed the ![]() ‘s are all in
‘s are all in ![]() , which may be only a subset of
, which may be only a subset of ![]() ‑ and this mapping may or may not be some
‑ and this mapping may or may not be some ![]() with
with ![]() a
a ![]() -morphism from
-morphism from ![]() to
to ![]() . This false reasoning arises precisely in the presentations by the author of direct products of representations, direct sums and subrepresentations. That will be for another post.
. This false reasoning arises precisely in the presentations by the author of direct products of representations, direct sums and subrepresentations. That will be for another post.