Definitions concerning filters
Definition of a filter
Let ![]() be a set.
be a set.
Traditional definition of a filter on ![]() : A collection
: A collection ![]() of subsets of
of subsets of ![]() is a filter on
is a filter on ![]() iff:
iff:
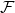 is non-empty (equivalently in context:
is non-empty (equivalently in context:  );
);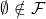 ;
;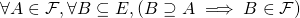 ;
;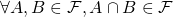 .
.
It follows from the definition that there can be no filters on the empty set.
If we waive the second rule and allow ![]() among elements of a filter, we obtain a hyperfilter on
among elements of a filter, we obtain a hyperfilter on ![]() . The only hyperfilter on
. The only hyperfilter on ![]() that is not a filter is
that is not a filter is ![]() , since if
, since if ![]() is an element, all supersets of
is an element, all supersets of ![]() must also belong.
must also belong.
Alternative equivalent definition
A collection ![]() of subsets of
of subsets of ![]() is a filter on
is a filter on ![]() iff
iff ![]() is non-empty; and
is non-empty; and ![]() ; and
; and ![]() .
.
Dispensing with the specification of the enclosing set
One can dispense with the specification of the enclosing set ![]() , retrieving it as
, retrieving it as ![]() . A filter is then a collection
. A filter is then a collection ![]() of sets such that:
of sets such that:
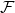 is non-empty;
is non-empty;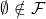 ;
;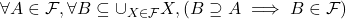 ;
;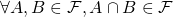 .
.
Fineness of filters
Definition: If ![]() and
and ![]() are filters on a same set
are filters on a same set ![]() , then
, then ![]() is finer than
is finer than ![]() iff
iff ![]() .
.
Filter bases and filter prebases
Definition: A collection ![]() of sets is a filter base iff:
of sets is a filter base iff:
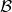 is non-empty;
is non-empty;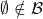 ;
;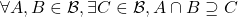 .
.
No enclosing set is specified.
It is trivial to check that a filter is always a filter base.
Filter generated by a filter base
If ![]() is a filter base and
is a filter base and ![]() a superset of all the elements of
a superset of all the elements of ![]() , let
, let ![]() be the set of all subsets of
be the set of all subsets of ![]() that are superset of some element of
that are superset of some element of ![]() :
:
![]()
It is trivial to check that ![]() is then a filter on
is then a filter on ![]() , and is a superset of
, and is a superset of ![]() .
.
By definition, ![]() is the filter generated on
is the filter generated on ![]() by
by ![]() .
.
Fineness of filter bases
Definition: If ![]() and
and ![]() are any two filter bases, then
are any two filter bases, then ![]() is finer than
is finer than ![]() iff every element of
iff every element of ![]() is a superset of some element of
is a superset of some element of ![]() .
.
Property: If ![]() and
and ![]() are filters on set
are filters on set ![]() and
and ![]() and
and ![]() filter bases that generate respectively
filter bases that generate respectively ![]() and
and ![]() , then
, then ![]() is finer than
is finer than ![]() iff
iff ![]() is finer than
is finer than ![]() .
.
Proof:
- Assume that
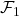 is finer than
is finer than 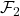 . Let
. Let 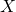 be an element of
be an element of 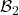 . It is then also an element of
. It is then also an element of 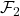 . Since
. Since  , we have
, we have 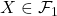 , and hence
, and hence 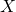 is a superset of some element of
is a superset of some element of  . This is true for all
. This is true for all  , hence
, hence  is finer than
is finer than 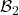 .
. - Assume that
 is finer than
is finer than 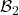 . Let
. Let 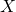 be an element of
be an element of 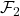 . Then
. Then 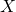 is superset of some element of
is superset of some element of 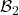 (since
(since 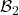 generates
generates 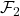 ), which itself (since
), which itself (since  is finer than
is finer than 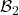 ) is a superset of some element of
) is a superset of some element of  , and thus is an element of
, and thus is an element of 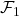 . This is true for all
. This is true for all 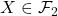 , hence
, hence 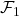 is finer than
is finer than 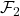 .
.
Equivalent filter bases
Definition: Two filter bases are equivalent if each is finer than the other.
Property: Two filter bases generate the same filter on a common enclosing set iff they are equivalent.
Proof: The generated filters are equal, that is, each finer than the other, iff their generating filter bases are each finer than the other, that is, equivalent.
Property: Equivalence is an equivalence relation among filter bases (trivial).
Filter prebases
A nonempty collection ![]() of sets is a filter prebase iff all finite intersections of elements of
of sets is a filter prebase iff all finite intersections of elements of ![]() are nonempty: for any finite and nonempty
are nonempty: for any finite and nonempty ![]() , we have
, we have ![]() .
.
If ![]() is a filter prebase, then together with all the finite intersections of its elements it forms a filter base.
is a filter prebase, then together with all the finite intersections of its elements it forms a filter base.
The image of a filter
Let ![]() and
and ![]() be sets,
be sets, ![]() a filter on
a filter on ![]() and
and ![]() .
.
Traditional definition: The filter on ![]() image of
image of ![]() by
by ![]() is
is ![]() .
.
Alternative definition: The filter on ![]() image of
image of ![]() by
by ![]() is
is ![]() .
.
Again, the two definitions are equivalent.