Direct sum of Hausdorff topological spaces

olivierd

Jul 19, 2017 3 min read

Direct sum of Hausdorff topological spaces

Exercise 185 (Chapter 28, “The category of topological spaces”):

Prove that both the direct product and the direct sum of two Hausdorff topological spaces is Hausdorff.

We will consider Hausdorff topological spaces $X$ and $Y$ and their direct sum (in the first part) or product (in the second part) $(Z, \alpha, \beta)$ .

We will proceed without reference to the explicit constructions of direct topological sums and products, using instead the results in “Theorems about the direct product and sum of two topological spaces”.

Direct sum

Let $c_1$ and $c_2$ be two eventual points of $Z$ , with $c_1 \neq c_2$ . The first result about direct sums in the above page implies that $\alpha^\rightarrow(X) \cap \beta^\rightarrow(Y) = \emptyset$ . The second result implies that $\alpha^\rightarrow(X) \cup \beta^\rightarrow(Y) = Z$ . Two cases are possible:

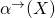One of $c_1$ and $c_2$ is in $\alpha^\rightarrow(X)$ and the other in $\beta^\rightarrow(Y)$ .
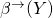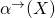Both $c_1$ and $c_2$ are in $\alpha^\rightarrow(X)$ , or both are in $\beta^\rightarrow(Y)$ .

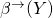We will consider successively the case where $c_1 \in \alpha^\rightarrow(X)$ and $c_2 \in\beta^\rightarrow(Y)$ , and the case where both are in $\alpha^\rightarrow(X)$ . The other possible cases are similar and will lead to similar results.

First case ( $c_1 \in \alpha^\rightarrow(X)$ and $c_2 \in\beta^\rightarrow(Y)$ ):

We have $c_1 = \alpha(a)$ and $c_2 = \beta(b)$ , with $a \in X$ and $b \in Y$ .

$X$ itself is an open neighbourhood of $a$ , and hence (last result about direct sums on the above page) $\alpha^\rightarrow(X)$ is an open neighbourhood of $c_1 = \alpha(a)$ in $Z$ . Similarly, $\beta^\rightarrow(Y)$ is an open neighbourhood of $c_2$ in $Z$ . Since $\alpha^\rightarrow(X)$ and $\beta^\rightarrow(Y)$ are disjoint, we have found disjoint neighbourhoods respectively of $c_1$ and $c_2$ .

Second case ( $c_1, c_2 \in \alpha^\rightarrow(X)$ ):

We have $c_1 = \alpha(a_1)$ and $c_2 = \alpha(a_2)$ , with $a_1, a_2 \in \alpha^\rightarrow(X)$ . Since $c_1 \neq c_2$ , we have $a_1 \neq a_2$ . Since $X$ is Hausdorff, there exist $U_1$ and $U_2$ disjoint open neighbourhoods in $X$ respectively of $a_1$ and $a_2$ .

//TODO (we need $\alpha$ injective)

Direct product

Let $c_1$ and $c_2$ be two eventual points of $Z$ , with $c_1 \neq c_2$ .

The first result about direct products in the above page implies that $\alpha(c_1) \neq \alpha(c_2)$ or $\beta(c_1) \neq \beta(c_2)$ .

Let us suppose that $\alpha(c_1) \neq \alpha(c_2)$ .

Since $X$ is Hausdorff and $\alpha(c_1)$ and $\alpha(c_2)$ are distinct points of $X$ , there exist open sets $U_1$ and $U_2$ of $X$ such that $\alpha(c_1) \in U_1$ , $\alpha(c_2) \in U_2$ and $U_1 \cap U_2 = \emptyset$ .

Then $\alpha^\leftarrow(U_1)$ and $\alpha^\leftarrow(U_2)$ are disjoint (the image by $\alpha$ of a common element would be both in $U_1$ and $U_2$ , which are disjoint). They are open (since $U_1$ and $U_2$ are open and $\alpha$ is continuous). Since $\alpha(c_1) \in U_1$ , we have $c_1 \in \alpha^\leftarrow(U_1)$ ; similarly, $c_2 \in \alpha^\leftarrow(U_2)$ . Thus there exist two disjoint open neighbourhoods respectively of $c_1$ and $c_2$ in $Z$ .

The same would result if we had $\beta(c_1) \neq \beta(c_2)$ .

This being the case for all $c_1, c_2 \in Z$ with $c_1 \neq c_2$ , the topological space $Z$ is Hausdorff.

exercise